| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 테스트
- 참조키
- querydsl
- 외부키
- 적용우선순위
- Query
- docker명령어
- appspec.yml
- ㅔㄴ션
- 추후정리
- 메세지수정
- 컨테이너실행
- EC2
- 메소드명
- appspec
- foreignkey
- 네이티브쿼리
- ubuntu
- 테스트메소드
- subquery
- AuthenticationEntryPoint
- 포트
- WeNews
- 2 > /dev/null
- application.yml
- 커밋메세지수정
- 예약
- 서브쿼리
- MySQL
- 검색
- Today
- Total
제뉴어리의 모든것
이진탐색트리 개념 본문
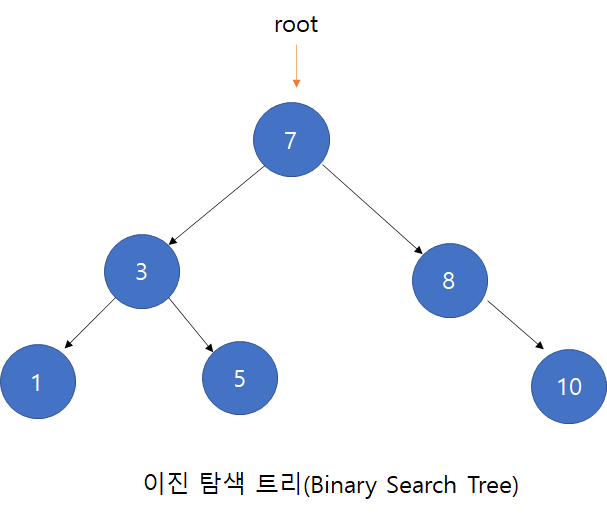
이진탐색트리(Binary Search Tree)이란?
이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다.
- 각 노드에 중복되지 않는 키(key)가 있다.
- 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.
- 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.
- 좌우 서브 트리도 모두 이진 탐색 트리여야 한다.
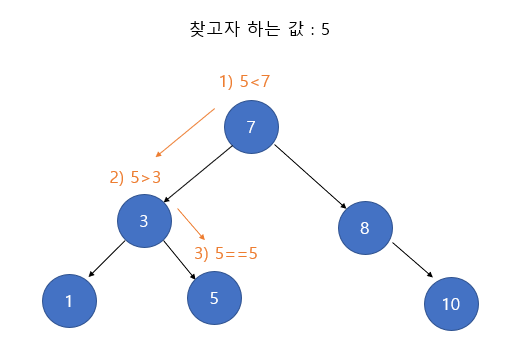
이진 탐색 트리 탐색(Search) 과정
- 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료한다.
- 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.
- 찾고자 하는 값이 루트노드의 키보다 크다면 오른쪽 서브트리로 탐색을 진행한다.
위 과정을 찾고자 하는 값을 찾을 때까지 반복해서 진행한다. 만약 값을 찾지 못한다면 그대로 종료한다.
이러한 탐색 과정을 거치면 최대 트리의 높이(h)만큼의 탐색이 진행되게 된다
코드상의 탐색 과정
TreeNode* search(TreeNode* root, int key){
if(root == NULL){ // 값을 찾지 못한 경우
return NULL;
}
if(key == root->key){ // 값을 찾음
return root;
}
else if(key < root->key){ // 왼쪽 서브트리 탐색
search(root->left, key);
}
else if(key > root->key){ // 오른쪽 서브트리 탐색
search(root->right, key);
}
}
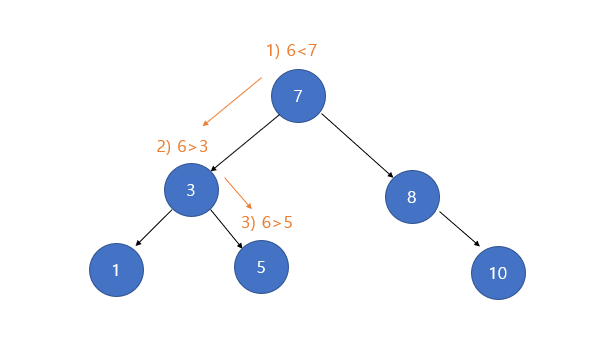
이진 탐색 트리 삽입(insert)
- 삽입할 값을 루트 노드와 비교해 같다면 오류를 발생한다( 중복 값 허용 X )
- 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.
- 삽입할 값이 루트노드의 키보다 크다면 오른쪽 서브트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.
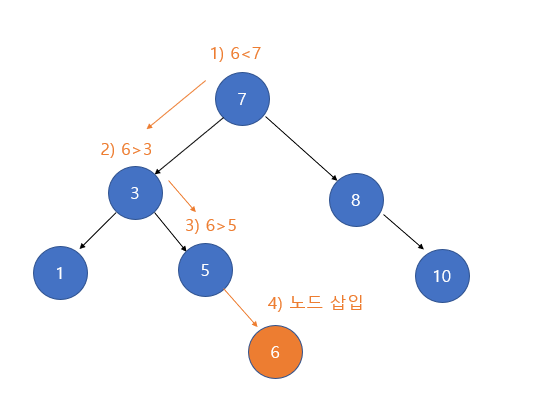
코드상의 삽입 과정
void insert(TreeNode** root, int key){
TreeNode* ptr; // 탐색을 진행할 포인터
TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode)); // newNode 생성
newNode->key = key;
newNode->left = newNode->right = NULL;
if(*root == NULL){ // 트리가 비어 있을 경우
*root = newNode;
return;
}
ptr = *root; // root 노드부터 탐색 진행
while(ptr){
if(key == ptr->key){ // 중복값
printf("Error : 중복값은 허용되지 않습니다!\n");
return;
}else if(key < ptr->key){ // 왼쪽 서브트리
if(ptr->left == NULL){ // 비어있다면 추가
ptr->left = newNode;
return;
}else{ // 비어있지 않다면 다시 탐색 진행
ptr= ptr->left;
}
}else{ // key > ptr->key 오른쪽 서브트리
if(ptr->right == NULL){ // 비어있다면 추가
ptr->right = newNode;
return;
}else{ // 비어있지 않다면 다시 탐색 진행
ptr = ptr->right;
}
}
}
}
이진 탐색 트리의 삭제(delete)
- 삭제하려는 노드가 단말 노드(leaf node) 일 경우
- 삭제하려는 노드의 서브 트리가 하나인 경우(왼쪽 혹은 오른쪽 서브 트리)
- 삭제하려는 노드의 서브 트리가 두 개인 경우
1. 삭제하려는 노드가 단말 노드(leaf node) 일 경우
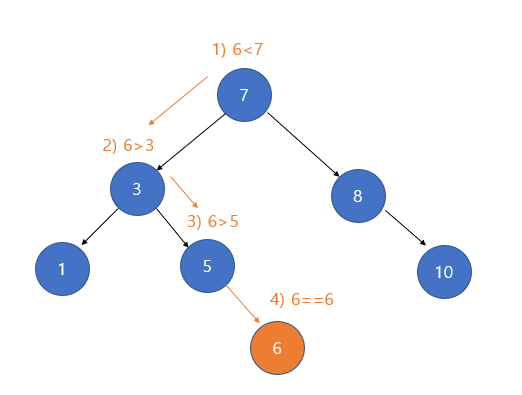
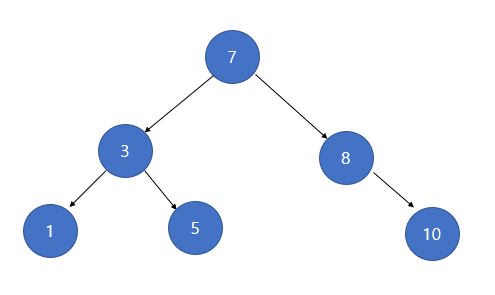
자식이 없는 단말 노드의 삭제는 간단하다. 삭제할 노드의 부모 노드가 있다면 부모 노드의 자식 노드를 NULL로 만들고, 삭제할 노드를 삭제(메모리 해제) 해주면 된다.
2. 삭제하려는 노드의 서브 트리가 하나인 경우(왼쪽 혹은 오른쪽 서브 트리)
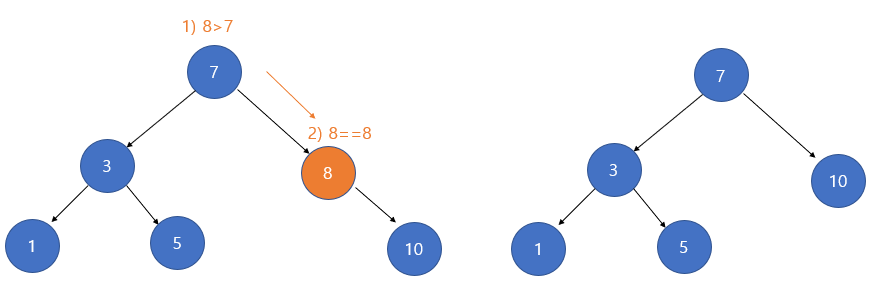
삭제하려는 노드의 서브 트리가 하나인 경우도 간단하다. 삭제할 노드의 자식노드를 삭제할 노드의 부모노드가 가리키게 하고 해당 노드를 삭제하면 된다.
3. 삭제하려는 노드의 서브트리가 두 개인 경우
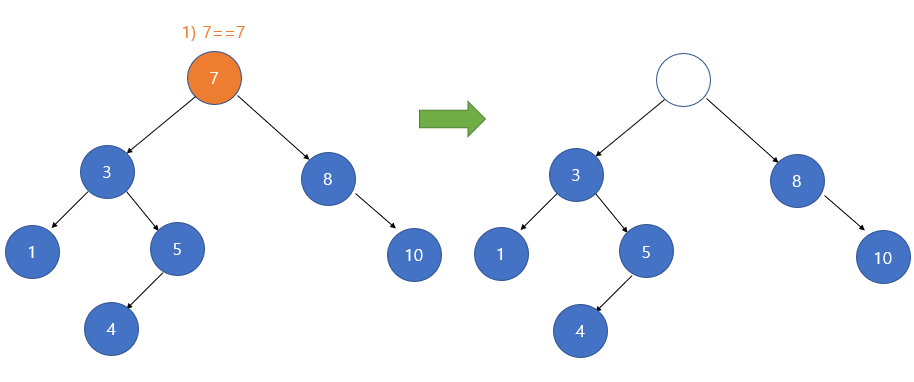
삭제하려는 노드의 서브트리가 두 개인 경우는 가장 복잡하다. 이 경우 두 가지 방법을 사용할 수 있다.
1) 삭제할 노드 왼쪽 서브 트리의 가장 큰 자손을 해당 노드의 자리에 올린다.
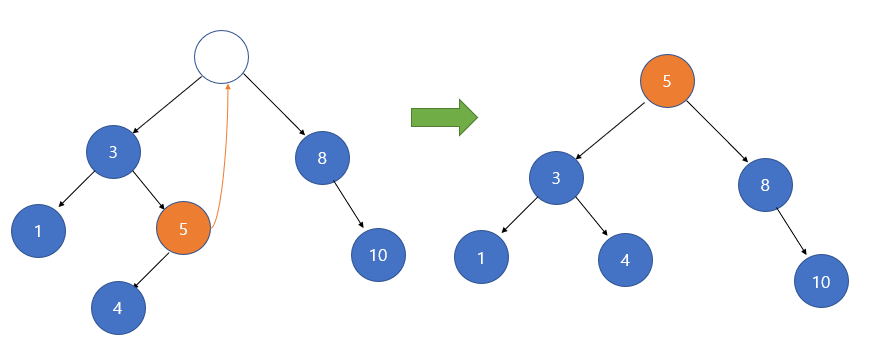
위와 같이 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 자손을 해당 노드의 자리에 올리면, 이진 탐색 트리의 조건을 만족하면서 트리가 유지되는 것을 확인할 수 있다. 또한 자리를 옮기면서 다른 노드들(4번노드)도 자리가 적절히 이동한 것을 확인 할 수 있다.
2) 삭제할 노드 오른쪽 서브 트리의 가장 작은 자손을 해당 노드의 자리에 올린다.
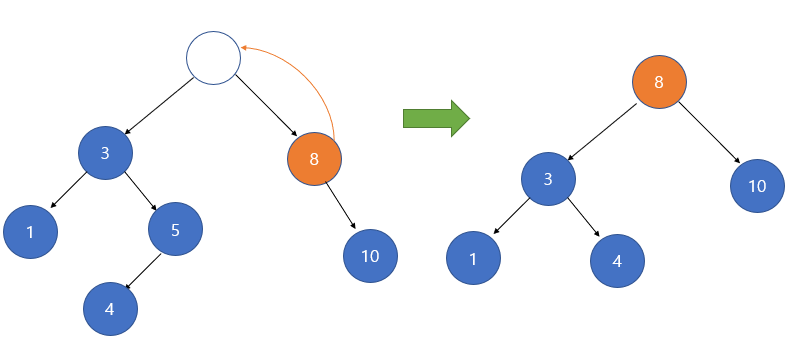
위와 같이 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 자손을 해당 노드의 자리에 올리면, 이진 탐색 트리의 조건을 만족하면서 트리가 유지되는 것을 확인할 수 있다. 또한 자리를 옮기면서 다른 노드들(10번노드)도 자리가 적절히 이동한 것을 확인 할 수 있다.
코드상의 삭제 과정
TreeNode* delete_node(TreeNode* root, int key){
TreeNode* del = NULL; // 삭제할 노드
TreeNode* parent = NULL; // 삭제할 노드의 부모 노드
TreeNode* successor = NULL; // 삭제할 노드의 왼쪽 서브트리에서 가장 큰 노드
TreeNode* predecessor = NULL; // successor의 부모노드
TreeNode* child = NULL; // 삭제할 노드의 자식 노드
del= root;
while(del != NULL){ // 삭제할 노드 탐색
if(key == del->key){
break;
}
parent = del;
if(key < del->key){
del = del->left;
}else{
del = del->right;
}
}
if(del == NULL){
printf("Error : 존재하지 않는 키\n");
return root;
}
if(del->left == NULL && del->right == NULL){ // 삭제할 노드의 자식노드가 없는 경우
if(parent != NULL){ // 부모노드가 있는 경우
if(parent->left == del){ // 부모노드의 왼쪽노드가 삭제할 노드일 때
parent->left = NULL;
}else{ // 오른쪽 일 때
parent->right = NULL;
}
}else{ // 부모노드가 없는 경우 = root 노드
root = NULL;
}
}else if(del->left != NULL && del->right != NULL){ // 삭제할 노드의 자식 노드가 2개인 경우
predecessor = del;
successor = del->left;
while(successor->right != NULL){ // 왼쪽 서브트리에서 가장 큰 값 찾기
predecessor = successor;
successor = successor->right;
}
predecessor->right = successor->left; // successor의 자식 노드 위치 변경
successor->left = del->left; // successor를 삭제할 노드의 위치로 옮긴 것과 같음
successor->right = del->right;
if(parent != NULL){ // 삭제할 노드의 부모노드가 있을 때
if(parent->left == del){
parent->left = successor;
}else{
parent->right = successor;
}
}else{
root = successor;
}
}else{ // 삭제할 노드의 자식 노드가 1개인 경우
if(del->left != NULL){ // 왼쪽 노드
child = del->left;
}else{ // 오른쪽 노드
child = del->right;
}
if(parent != NULL){ // 부모노드가 있는 경우
if(parent->left == del){ // 부모노드의 왼쪽 노드로 삭제할 노드의 자식노드 연결
parent->left = child;
}else{ // 부모노드의 오른쪽 노드로 삭제할 노드의 자식노드 연결
parent->right = child;
}
}else{
root = child;
}
}
free(del); // 메모리해제
return root;
}
참조
'알고리즘' 카테고리의 다른 글
| [프로그래머스] 게임 맵 최단거리 [BFS/DFS] (0) | 2023.02.28 |
|---|---|
| 이진탐색트리 순회 개념 (0) | 2023.01.05 |
| 자료구조 트리 개념 (0) | 2023.01.05 |
| 자료구조 그래프 개념 (1) | 2022.12.30 |
| PowerSet (부분집합) 문제 (0) | 2022.10.09 |




