| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 참조키
- 외부키
- EC2
- MySQL
- 2 > /dev/null
- 테스트메소드
- 포트
- 예약
- application.yml
- foreignkey
- 서브쿼리
- 추후정리
- 적용우선순위
- Query
- appspec.yml
- 메소드명
- ㅔㄴ션
- 커밋메세지수정
- querydsl
- WeNews
- docker명령어
- 테스트
- 검색
- appspec
- subquery
- 컨테이너실행
- 메세지수정
- AuthenticationEntryPoint
- 네이티브쿼리
- ubuntu
- Today
- Total
제뉴어리의 모든것
자료구조 그래프 개념 본문
1. 그래프
그래프(Graph)는 연결되어있는 원소간의 관계를 표현한 자료구조입니다.

그래프
· 그래프는 연결할 객체를 나타내는 정점(Vertext)과 객체를 연결하는 간선(Edge)의 집합으로 구성됩니다.
· 그래프 G를 G=(V, E)로 정의하는데, V는 정점의 집합, E는 간선들의 집합을 의미합니다.
2. 그래프 종류
① 무방향 그래프
무방향 그래프(Undirected Graph)는 두 정점을 연결하는 간선에 방향이 없는 그래프.
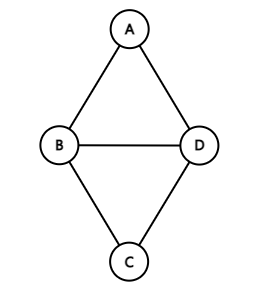
무방향 그래프 G1
· 무향방 그래프에서 정점 Vi와 Vj를 연결하는 간선을 (Vi, Vj)로 표현하는데, 이때 (Vi, Vj)와 (Vj, Vi)는 같은 간선을 나타냅니다.
· V(G1)={A,B,C,D}, E(G1)={(A,B), (A,D), (B,C), (B,D), (C,D)}
② 방향 그래프
방향 그래프(Directed Graph)는 간선에 방향이 있는 그래프.
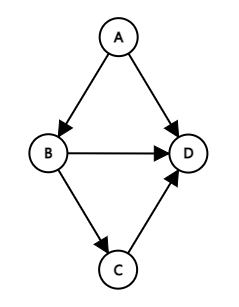
방향 그래프 G2
· 방향 그래프에서 정점 Vi와 Vj를 연결하는 간선을 <Vi, Vj>로 표현하는데 Vi를 꼬리(tail), Vj를 머리(head)라고 합니다. 이때 <Vi, Vj>와 <Vj, Vi>는 서로 다른 간선입니다.
· V(G1)={A,B,C,D} E(G1)={<A,B>, <A,D>, <B,C>, <B,D>, <C,D>}
③ 완전 그래프
완전 그래프(Complete Graph)는 한 정점에서 다른 모든 정점과 연결되어 최대 간선 수를 갖는 그래프.
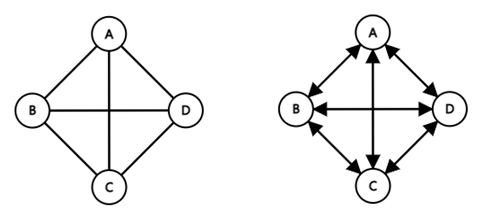
완전 그래프 G3와 G4
· 정점이 n개인 완전 그래프에서 무방향 그래프의 최대 간선 수는 n(n-1)/2이고 방향 그래프의 최대 간선 수는 n(n-1)입니다.
④ 부분 그래프
부분 그래프(Subgraph)는 기존의 그래프에서 일부 정점이나 간선을 제외하여 만든 그래프.
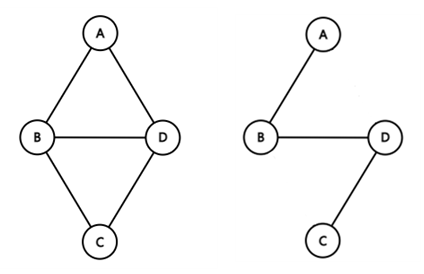
그래프 G5과 부분 그래프 G5'
⑤ 가중 그래프
가중 그래프(Weight Graph)는 정점을 연결하는 간선에 가중치(weight)를 할당한 그래프.
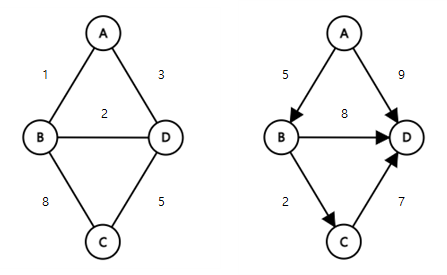
가중치 그래프 G6과 G7
⑥ 유향 비순환 그래프(DAG, Directed Acyclic Graph)
방향 그래프에서 사이클이 없는 그래프.
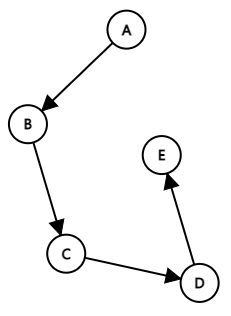
유향 비순환 그래프 G8
⑦ 연결 그래프(Connected Graph)
떨어져 있는 정점이 없는 그래프.
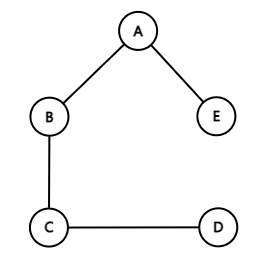
연결 그래프 G9
⑧ 단절 그래프(Disconnected Graph)
연결되지 않은 정점이 있는 그래프.
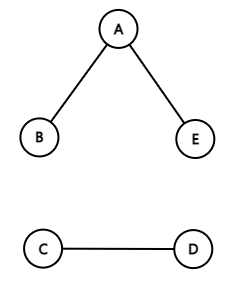
단절 그래프 G10
3. 그래프 용어
그래프에서 두 정점 Vi와 Vj가 연결되어 간선 (Vi, Vj)가 있을 때, 두 정점 Vi와 Vj를 인접(adjacent)한다 하고, 간선 (Vi, Vj)는 정점 Vi와 Vj에 부속(incident)되어 있다고 말합니다.
- 차수(Dgree): 정점에 부속되어 있는 간선의 수
-진입차수(in-degree): 정점을 머리로 하는 간선의 수
-진출차수(out-degree): 정점을 꼬리로 하는 간선의 수
- 경로(Path): 정점 Vi에서 Vj까지 간선으로 연결된 정점을 순서대로 나열한 리스트
-단순 경로(Simple Path): 모두 다른 정점으로 구성된 경로
- 경로 길이(Path Length): 경로를 구성하는 간선의 수
- 사이클(Cycle): 단순 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로
- 인접 정점(adjacent Vertex) : 간선에 의해 직접 연결된 정점
- 사이클(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우
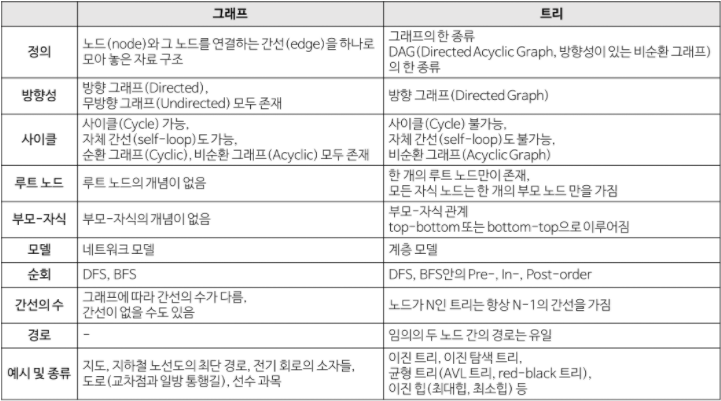
4. 트리와의 차이
그래프는 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조이다.
정확히는 정점(Vertex)간의 관계를 표현하는 조직도라고 볼 수 있다.
이러한 면에서 트리는 그래프의 일종인 셈이다. 하지만 그래프는 트리와는 달리 정점마다 간선이 있을 수도 있고 없을 수도 있으며, 루트노드와 부모와 자식이라는 개념이 존재하지 않는다.
그래프와 트리의 차이 차트
5. 그래프 구현 방법
그래프를 구현하는 방법에는 인접행렬과 인접리스트 방식이 있다.
- 인접행렬 방식
인접행렬은 그래프의 노드를 2차원 배열로 만든 것이다.
노드들 간에 직접 연결이 되어있으면 1을, 아니면 0을 넣어서 행렬을 완성시킨 것이다. - 인접행렬의 장점
- 2차원 배열 안에 모든 정점들의 간선 정보가 담겨있기 때문에 두 정점에 대한 연결 정보를 조회할 때 O(1) 의 시간복잡도면 가능하다.
- 인접리스트에 비해 구현이 쉽다.
- 인접행렬의 단점
- 모든 정점에 대해 간선 정보를 대입해야 하므로 $O(n^2)$ 의 시간복잡도가 소요된다.
- 무조건 2차원 배열이 필요하기 때문에 필요 이상의 공간이 낭비된다.

- 인접리스트 방식
인접리스트는 그래프의 노드를 리스트로 표현한 것이다.
주로 정점의 리스트 배열을 만들어 관계를 설정하며 노드들 간에 직접 연결이 되어있으면 해당 노드의 인덱스에 그 노드를 삽입해주면 된다.
즉, 1에는 2와 3이 직접 연결되어 있기 때문에 배열의 1번째 칸에 2와 3을 넣어준다.
- 인접리스트의 장점
- 정점들의 연결 정보를 탐색할 때 O(n) 시간이면 가능하다.
- 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
- 인접리스트의 단점
- 특정 두 점이 연결되었는지 확인하려면 인접행렬에 비해 시간이 오래걸린다. (O(E) 시간 소요. E는 간선의 개수)
- 구현이 비교적 어렵다.
참조 :
https://leejinseop.tistory.com/43
https://hongcoding.tistory.com/78
깊이 우선 탐색
https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs.html
너비 우선 탐색
https://kingpodo.tistory.com/48
그래프 구현
'알고리즘' 카테고리의 다른 글
| 이진탐색트리 개념 (0) | 2023.01.05 |
|---|---|
| 자료구조 트리 개념 (0) | 2023.01.05 |
| PowerSet (부분집합) 문제 (0) | 2022.10.09 |
| [dp] 백준 2293 동전1 (0) | 2022.09.29 |
| 백준 17478 - 재귀함수가 뭔가요? (재귀) (0) | 2022.07.24 |


