| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- subquery
- ubuntu
- 커밋메세지수정
- EC2
- ㅔㄴ션
- 테스트
- querydsl
- 컨테이너실행
- Query
- 서브쿼리
- 외부키
- 테스트메소드
- 예약
- 검색
- MySQL
- application.yml
- 메소드명
- 적용우선순위
- 참조키
- WeNews
- 추후정리
- 2 > /dev/null
- docker명령어
- 포트
- foreignkey
- appspec.yml
- 네이티브쿼리
- 메세지수정
- appspec
- AuthenticationEntryPoint
- Today
- Total
제뉴어리의 모든것
[Section2] [코딩테스트 준비] 탐욕 알고리즘 (Greedy) 본문
그리디 알고리즘이란?
탐욕 알고리즘으로도 불리며, 매순간 현재 이 순간 최선의 상황만을 쫓아 해답에 도달하는 방식의 알고리즘.
그리디 알고리즘으로 문제 해결 절차
- 선택 절차(Selection Procedure): 현재 상태에서의 최적의 해답을 선택합니다.
- 적절성 검사(Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사합니다.
- 해답 검사(Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복합니다.
예를 들어 설명하자면,
내가 편의점 점주이고, 고객이 440원짜리 물건을 사면서 1000원을 냈을때,
나는 500원, 100원, 50원, 10원 짜리 동전을 무한히 가지고 있다고 하자.
그럼 거스름돈은 560원일것이다.
이때, 내가 고객에게 거스름돈으로 줄 돈전의 갯수를 최소로 주어야 한다면?
여러 경우의 수가 있을것이다.
100원 X 5, 10원 X 6개 로도 가능하다. 하지만
최소갯수여야 하기 때문에 틀렷다.
이럴때 그리디방식을 쓰면
제일 높은 금액의 동전을 최대한 주고 그다음 더이상 줄 수 없을때 한단계 작은 단위의 동전을 주고,
이러한 방법을 반복한다.
그래서 정답은 500원 X 1, 50원 X 1, 10원 X 1일 것이다.
그리디 알고리즘 단점
- 전체 문제의 부분 문제가 서로의 문제에 영향을 미치는 경우
최적에 근사한 값일 수는 있지만, 최적의 해가 아닐 수가 있다.
그리디 알고리즘 가능 조건
-
탐욕 선택 속성(greedy choice property)
탐욕적인 선택은 항상 안전하다는 것이 보장되어야 합니다. 여기서 "안전하다"라는 것은 이 선택으로 인해 전체 문제의 최적해를 반드시 도출할 수 있어야 한다는 것입니다. -
최적 부분 구조(optimal substructure)
문제에 대한 최종 해결 방법이 부분 문제에 대해서도 또한 최적의 해결 방법이다라는 조건입니다.
쉽게 말해, 현재의 선택이 다음 선택에 전혀 영향을 미치지 않아야 하며, 전체 문제를 부분 문제로 나눴을때!
각 부분문제들의 최적 해답의 합이 전체 문제의 최적 해답이 가능한 경우에 그리디 알고리즘으로 풀 수가 있다는것이다.
말이 너무 어렵다. 예를 들어 설명하지 않으면 위에 글로만은 이해하기 어렵다.
그리고 글로써는 이보다 더 쉽게 설명할 길이 없을것 같다
그러므로 자세한 내용은 아래를 보자.
- 사례 1
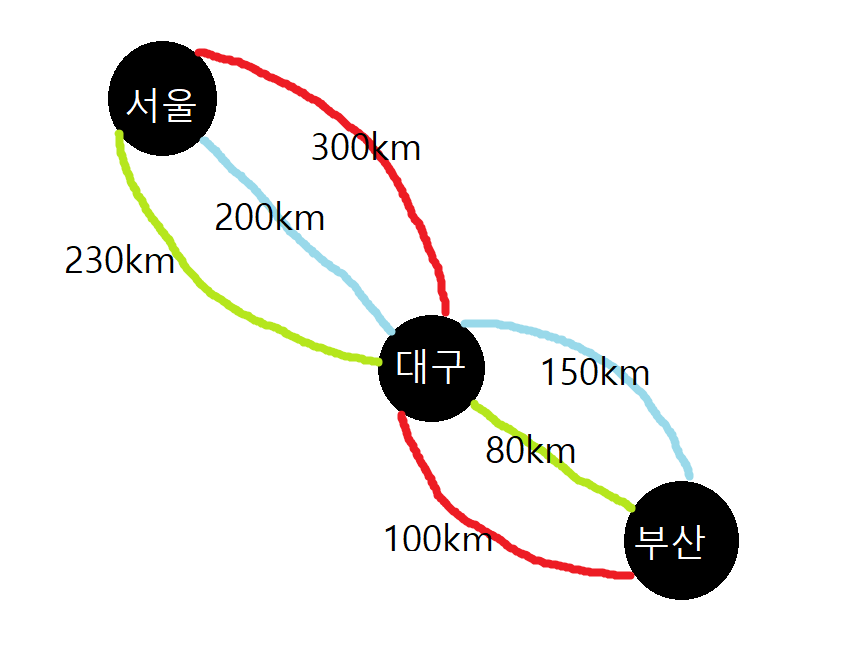
위와 같이 서울에서 대구, 대구에서 부산을 가는 경로가 나와있다.
이때 아래와 같은 문제가 있다 생각해보자.
- 원래 문제 :(아무런 조건없이) 서울에서 부산을 갈 수 있는 최단거리 (최적해답) 를 구하라고 한다면,
서울에서 대구를 가는 방법 중 어디를 가든 상관이 없으니, 제일 짧은 거리인 200km 경로로 가고,
대구에서 부산을 가는 경로중 가장 짧은 80km 경로로 가서
총 280km 구간이 될것이다!
이렇듯, 전체 문제인 서울~부산 가는 방법의 부분 문제인 서울~대구 경로와, 대구~부산 경로는 서로
영향을 미치지 않는다.
즉, 서울에서 대구까지의 가는 경로들중 무엇으로 왔든, 대구에서 부산을 가는 경로를 선택할때 아무런 영향을 끼치지 않으며, 서울~대구 경로 선택시 최적의해 + 대구~부산 경로 선택시 최적의해 가 곧 전체의 최적해가 된다.
위에서 말한
"쉽게 말해, 현재의 선택이 다음 선택에 전혀 영향을 미치지 않아야 하며, 전체 문제를 부분 문제로 나눴을때!
각 부분문제들의 최적 해답의 합이 전체 문제의 최적 해답이 가능한 경우에 그리디 알고리즘으로 풀 수가 있다는것이다."
라는 말에 다 해당이 되는 조건의 문제이다.
그러므로 그리디 알고리즘으로 최적해를 구할 수있는 문제 유형이라고 할 수있겠다.
그러나!
위에 문제에서 조건만 하나가 달린다면,
그리디 알고리즘으로 풀 수 없는 문제가 되버린다.
그조건은 무엇이냐면
"서울~부산 으로 향할때 한 민간기업이 지은 도로로만 갈 수 있다" 라는 조건이 걸린다면!
그리디로 최적의 해를 찾을 수 없게된다.
그럼 조건을 추가하여 그리디로 풀었던 위에 문제를 못푸는 상황을 만들어보자.
- 수정된 문제 :
서울~부산을 가는 최단 경로를 구하여라. 단, 한 건설사가 지은 도로로만 갈 수 있다.
위 그림에서 건설사의 구별은 경로의 색깔로 구별한다.
라는 문제일때, 그리디 방식으로 풀어보자.
서울~대구 경로 중 가장 짧은 경로는 200km 하늘색 경로이다.
그리고 대구~부산 경로 중 가장 짧은 경로는 80km의 경로이다.
그러나 녹색 경로 이므로 하늘색 경로를 지은 건설사가 아니다.
그래서 같은 건설사가 지은 하늘색 경로 150km 경로로 가야한다.
그럼 최종 서울~부산 경로의 거리는 350km 이다...
서울~대구 경로에서 최적의 해를 선택하였다고 해서, 전체적으론 최적의 해가 아니며,
서울~대구 경로의 선택이 이후 대구~부산 경로 선택에 영향을 미쳤다.
그러므로 이 수정된 문제는 그리디로 풀 수 없는 문제되었다.
사례 2
- 원래 문제 :
나는 편의점 점주이다. 손님이 15원짜리 물건을 사며 100원을 냈다.
나는 1원, 5원, 20원, 40원의 가치를 하는 동전을 갖고 있으며 각 동전의 수는 무한하다. (각 동전은 문제를 위한 가상의 동전이다.)
이때, 가지고 있는 동전을 사용하여 85원을 거슬러 주어야하는데, 최소 갯수의 동전으로 거스름돈을 반환하라.
라는 문제가 있다고 하자.
그리디 알고리즘을 사용하면
단순히 40원짜리 동전 2개와 5원짜리 1개를 거슬러 주면 된다. (총 3개)
- 수정된 문제 :
그러나, 만약 가지고 있는 동전의 종류가 아래와 같이 다를 경우를 생각해보자.
내가 가지고 있는 동전이
1원, 5원, 20원, 27원 일때 85원을 거슬러 주어야 한다면 어떨까.
그리디 알고리즘을 그대로 적용하면
27원 3개 -> 거스름돈 4원 남음
1원 4개 -> 거스름돈 0원 남음
총 7개의 동전을 사용하게 된다.
즉, 그리디 알고리즘으로 풀 수 없는 문제가 된다.
"쉽게 말해, 현재의 선택이 다음 선택에 전혀 영향을 미치지 않아야 하며, 전체 문제를 부분 문제로 나눴을때!
각 부분문제들의 최적 해답의 합이 전체 문제의 최적 해답이 가능한 경우에 그리디 알고리즘으로 풀 수가 있다는것이다."
라는 조건에 충족하지 않는다.
거스름돈을 큰 단위의 동전에서 작은 단위에 동전으로 으로 나누는 단계의 부분문제들의 최적해의 합이 전체 문제의 최적합과 맞지 않는것이다.
이런 경우의 문제에선
각 동전의 단위가 배수 관계가 아닐때 그리디 알고리즘을 사용해야할지 고민해봐야한다.
원래 문제에선 1원의 5배인 5원, 5원의 4배인 20원, 20원의 2배인 40원으로 구성되어 있었지만,
수정된 문제에선 1원, 5원, 20원, 27원으로 27원이 20원과의 배수관계가 이루어지지 않는다.
이 의미는 무엇이냐면, 어떤 동전을 선택하느냐에 따라 다른 동전을 선택하지 못하는 경우가 발생한다는것이다.
동전이 배수로만 존재할때는 (1, 5, 20, 40) 만약 40원을 1개만 선택했고 40원이 남는다고 하면
나머지 금액을 20원짜리만으로도 채울 수 있으며, 5원짜리 만으로도, 1원짜리 만으로도 채울 수도 있다.
그러나, 수정된 문제처럼 동전이 존재할땐(1, 5, 20, 27) 27원이 하나 선택됬을때,
1원만으로는 채울 수 있지만, 5원만으로는 채울수없고, 20원만으로도 채울 수 없다.
물론 27원만으로도 채울 수 없다.
즉, 현재 문제에서 27원을 선택함으로 다른 부분 문제의 선택에 영향을 미치게 된것이다.
그리고 부분문제의 최적 해답(가장 큰 단위 동전 선택) 이 전체 문제의 최적 해답으로도 이루어지지 않는다.
결론
알고리즘 문제를 만났을때, 전체를 문제를 부분문제로 나눠보고 그 부분 문제의 선택이 다른 부분 문제에 영향을 미치는가 생각해본다. 그리고, 부분 문제때마다 선택하는 해답들의 합이 전체 문제의 최적 해답이 될지 고민해봐야한다.
결론은 이렇지만, 실제로 문제를 보고 바로 파악하긴 힘들것이다.
그러므로, 예시의 입풋 말고도 여러가지 반례를 생각해보고 위에서 말한 조건들에 다 충족되는지 확인하고 그리디 알고리즘을 써야할 것이다.
탐욕법(그리디) 알고리즘
탐욕법(이하 '그리디') 알고리즘이란 현재 상황에서 가장 좋은 것(최선의 선택)을 고르는 알고리즘을 말합니다. 그리디 알고리즘은 동적 프로그래밍을 간단한 문제 해결에 사용하면 지나치게 많
velog.io
https://namu.wiki/w/%EA%B7%B8%EB%A6%AC%EB%94%94%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://www.youtube.com/watch?v=LD4AKF9tjro
[알고리즘] 탐욕 알고리즘(Greedy Algorithm) - 하나몬
❗️탐욕 알고리즘(Greedy Algorithm)이란? Greedy는 ‘탐욕스러운, 욕심 많은’ 이란 뜻이다. 탐욕 알고리즘은 말 그대로 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에
hanamon.kr
'코드스테이츠 > 정리 블로깅' 카테고리의 다른 글
| [Section2] [관계형 데이터베이스] 데이터베이스 정규화 [추후 정리] (0) | 2022.08.08 |
|---|---|
| [Section2] [네트워크] 웹 애플리케이션 작동원리 (0) | 2022.08.03 |
| [Section2] [코딩 테스트 준비] 자료구조 - 의사코드 (0) | 2022.07.29 |
| [Section2][자료구조/알고리즘] 자료구조 - BFS / DFS (0) | 2022.07.28 |
| [Section2][자료구조/알고리즘] 자료구조 - Tree traversal (0) | 2022.07.27 |


