| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Query
- 서브쿼리
- appspec.yml
- EC2
- 테스트
- 검색
- subquery
- 외부키
- 2 > /dev/null
- 적용우선순위
- ㅔㄴ션
- 테스트메소드
- 커밋메세지수정
- AuthenticationEntryPoint
- ubuntu
- docker명령어
- appspec
- application.yml
- 포트
- 추후정리
- 메소드명
- 컨테이너실행
- WeNews
- MySQL
- 예약
- 메세지수정
- foreignkey
- 네이티브쿼리
- querydsl
- 참조키
- Today
- Total
제뉴어리의 모든것
Heap 본문
=> 힙이란
우선순위 큐를 위해 만들어진 자료구조.
- 우선순위 큐란?
우선순위의 개념을 큐에 도입한 자료구조.
데이터들은 우선순위를 가지고 있고 우선순위가 높은 데이터가 먼저 나간다.
- 우선순위 큐의 구현
배열, 연결리스트, 힙으로 구현이 가능하다.
이중 힙으로 구현하는 것이 가장 효율적.
=> 힙의 자세한 정의
- 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.
- 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
- 힙은 일종의 반정렬 상태를 유지한다.
- 힙트리에서는 중복된 값을 허용한다.
- Full Binary Tree로 구성
Funn Binary Tree란 마지막 레밸을 제외한 나머지 레밸들은 노드가 꽉 차있어야 한다.
=> 힙의 종류
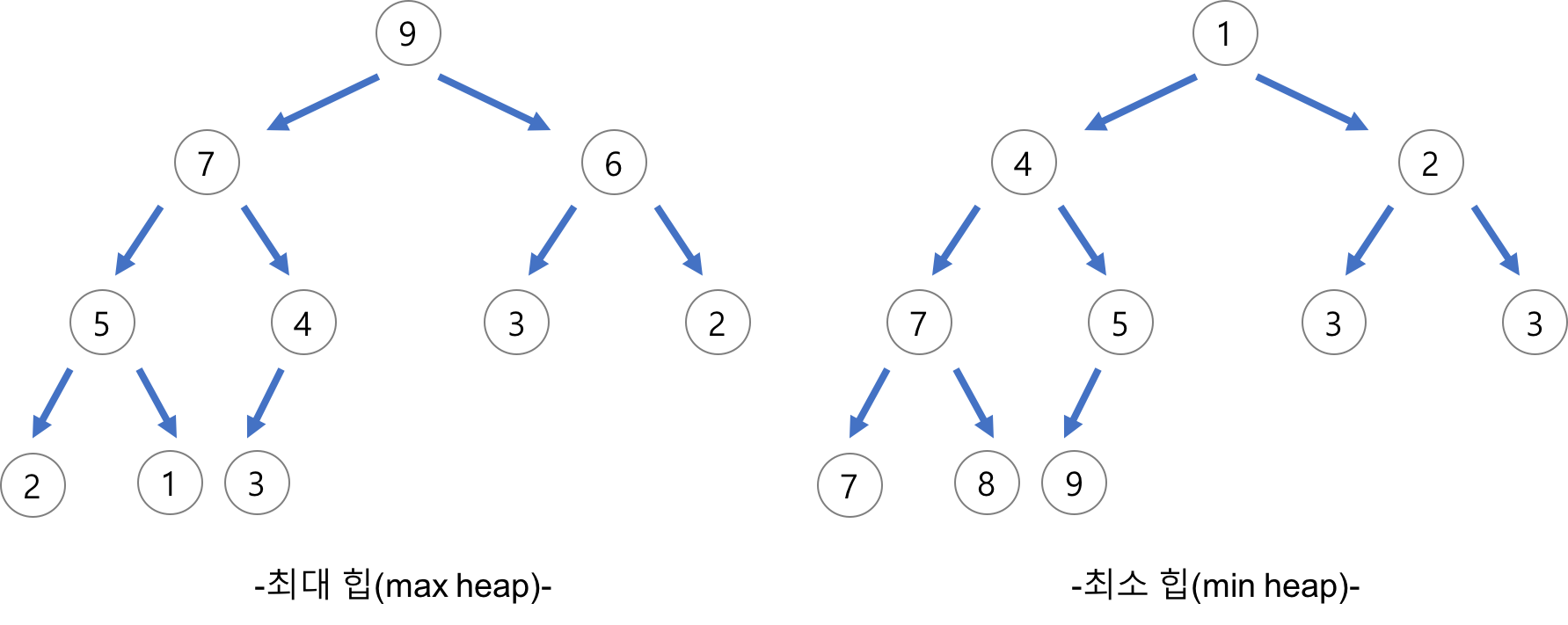
- 최대 힙
부모 노드의 키값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
부모 노드의값 >= 자식 노드의 값
- 최소힙
부모 노드의 키값이 나식 노드의 키 값보다 작거나 같은 완전 이진 트리
부모 노드값 <= 자식 노드의 값
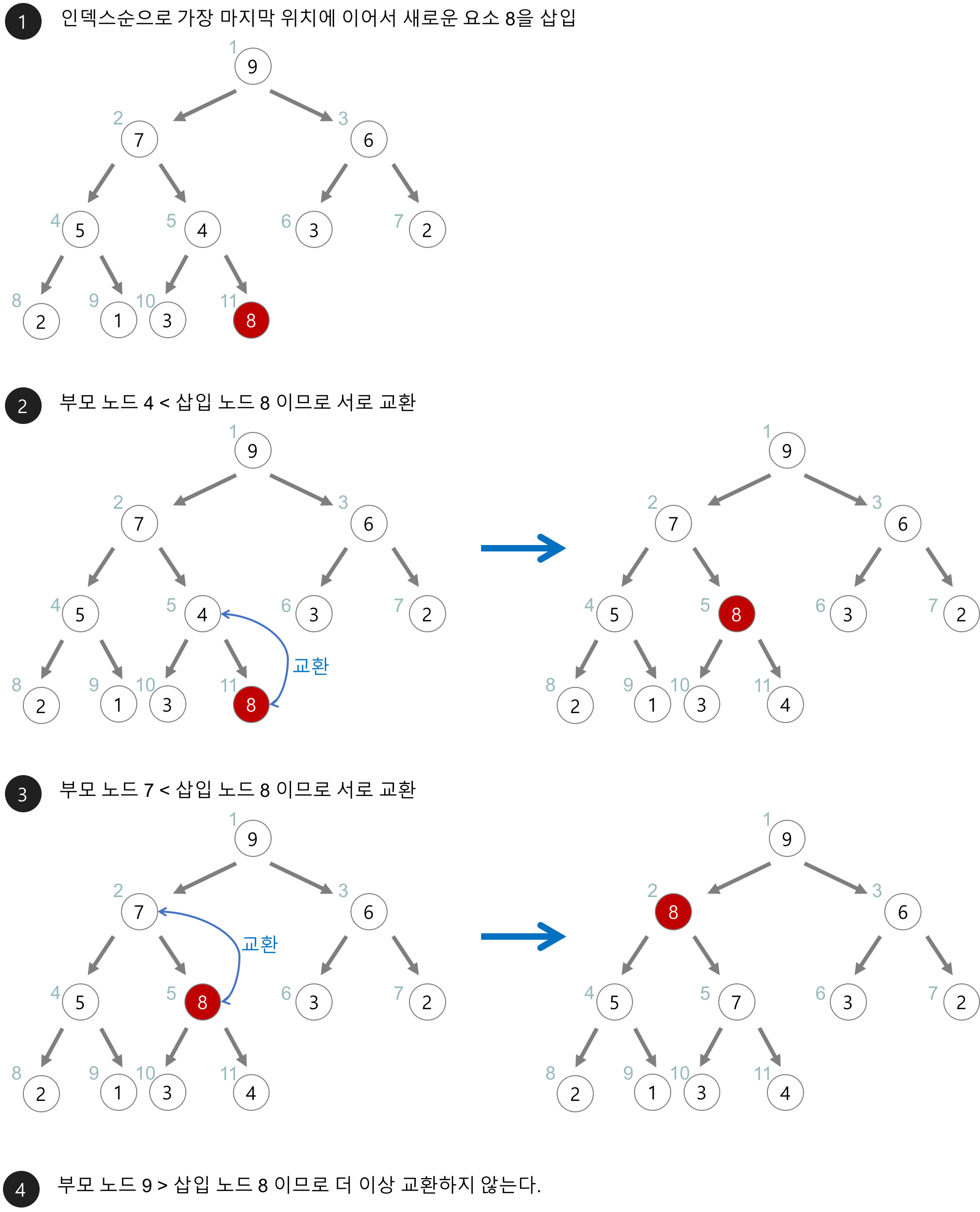
=> 힙(heap)의 삽입
- 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
- 아래의 최대 힙(max heap)에 새로운 요소 8을 삽입해보자.
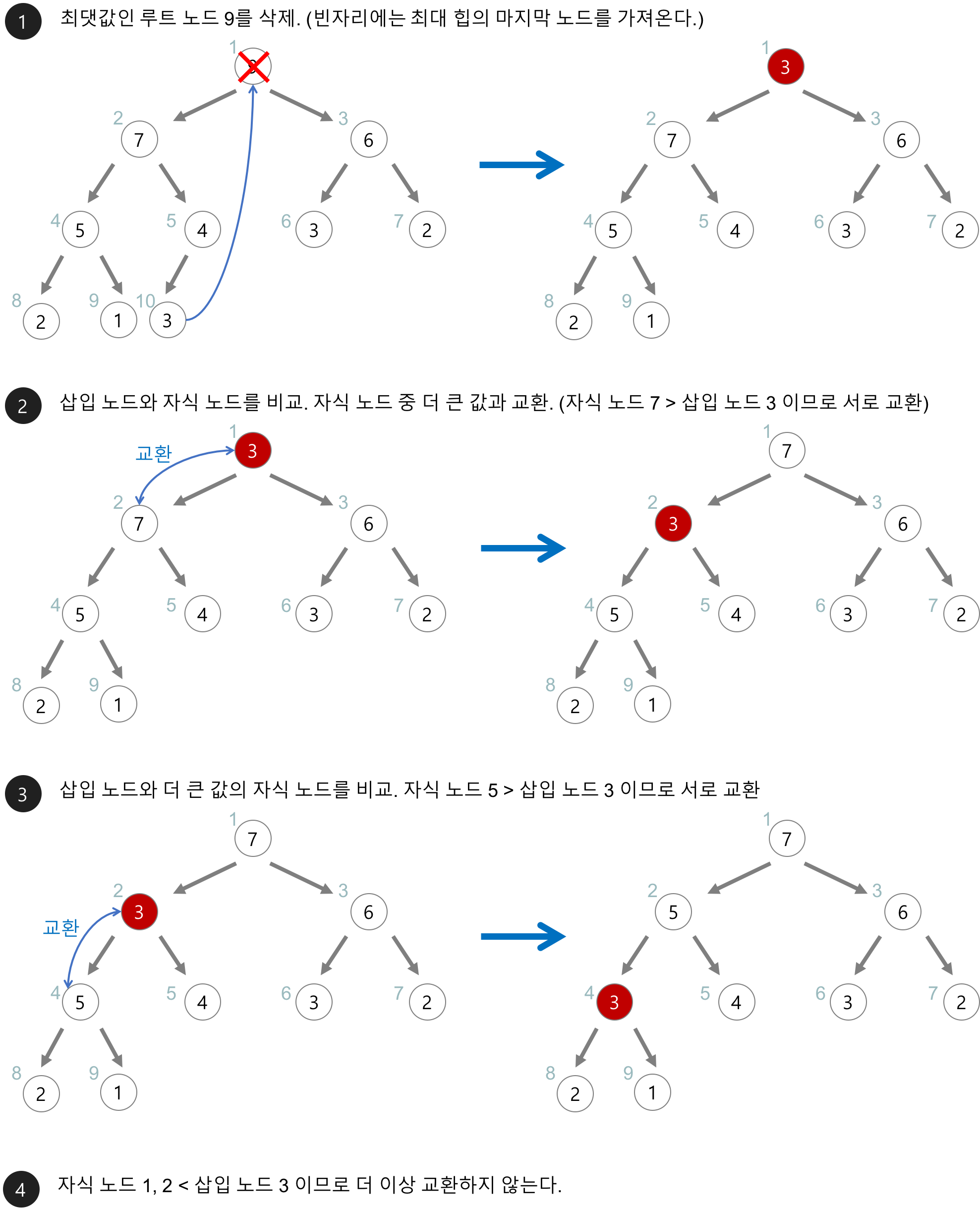
=> 힙(heap)의 삭제
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
- 최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.
- 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
- 힙을 재구성한다.
- 아래의 최대 힙(max heap)에서 최댓값을 삭제해보자.
=> 주의할점
=> 힙의 종류 파트의 이미지에서 나오듯이 특정 노드 기준으로 하위단의 노드가 무조건 특정 노드(상위노드)의 값보다 낮거나 높은것은 아니다.
위와 같이 최대힙의 상황에서 3은 2보다 값이 높지만 아랫단에 존재한다.
왜냐하면 소트의 기준이 무조건 부모와의 비교이고, 최초 삽입시에는 가장 아랫단에 좌측부터 시작하기 넣어주기 때문이다.
구현 내 코드 (JAVA)
package main;
public class main {
public static void main(String[] args) {
heap testHeap = new heap(200, heap.h_type.MIN);
System.out.println();
insertHeap(testHeap,100);
print(testHeap);
insertHeap(testHeap,19);
print(testHeap);
insertHeap(testHeap,36);
print(testHeap);
insertHeap(testHeap,25);
print(testHeap);
insertHeap(testHeap,101);
print(testHeap);
}
public static void insertHeap(heap desHeap, int insertValue)
{
node istNode = new node(insertValue);
if(desHeap.type == heap.h_type.MAX)
{
desHeap.heap[++desHeap.idx] = istNode;
//소팅
int curIdx = desHeap.idx;
for(int i = desHeap.idx/2; i > 0; i/=2)
{
if(desHeap.heap[curIdx].value > desHeap.heap[i].value)
{
swap(desHeap, i, curIdx);
curIdx = i;
}
}
}
else
{
desHeap.heap[++desHeap.idx] = istNode;
//소팅
int curIdx = desHeap.idx;
for(int i = desHeap.idx/2; i > 0; i/=2)
{
if(desHeap.heap[curIdx].value < desHeap.heap[i].value)
{
swap(desHeap, i, curIdx);
}
}
}
}
public static node removeHeap(heap desHeap)
{
node result = null;
result = desHeap.heap[1];
desHeap.heap[1] = desHeap.heap[desHeap.idx];
desHeap.heap[desHeap.idx] = null;
desHeap.idx--;
//소팅
int curIdx = 1;
if(desHeap.type == heap.h_type.MAX)
{
for(int i = curIdx * 2; i <= desHeap.idx; i = curIdx * 2)
{
int biggerIdx = i;
if(desHeap.heap[i+1] != null)
{
biggerIdx = desHeap.heap[i].value > desHeap.heap[i+1].value ? i : i + 1;
}
if(desHeap.heap[curIdx].value < desHeap.heap[biggerIdx].value)
{
swap(desHeap, curIdx, biggerIdx);
curIdx = biggerIdx;
}
else
{
break;
}
}
}
else
{
for(int i = curIdx * 2; i <= desHeap.idx; i = curIdx * 2)
{
int smallerIdx = i;
if(desHeap.heap[i+1] != null)
{
smallerIdx = desHeap.heap[i].value < desHeap.heap[i+1].value ? i : i + 1;
}
if(desHeap.heap[curIdx].value > desHeap.heap[smallerIdx].value)
{
swap(desHeap, curIdx, smallerIdx);
curIdx = smallerIdx;
}
else
{
break;
}
}
}
return result;
}
public static void swap(heap desHeap, int parIdx, int cldIdx)
{
node tempNode = desHeap.heap[parIdx];
desHeap.heap[parIdx] = desHeap.heap[cldIdx];
desHeap.heap[cldIdx] = tempNode;
}
public static void print(heap desHeap)
{
for(int i = 1; i <= desHeap.idx; i++)
{
System.out.print(desHeap.heap[i].value);
if(i != desHeap.idx)
System.out.print(" ");
}
System.out.println();
}
}
class node
{
int value;
public node(int value) {
this.value = value;
}
}
class heap
{
enum h_type
{
MAX,
MIN
}
node[] heap;
int heapSize;
h_type type;
int idx;
public heap(int heapSize, h_type type) {
this.idx = 0;
this.heap = new node[heapSize];
this.heapSize = heapSize;
this.type = type;
}
public void setHeap(node[] heap) {
for(int i = 0; i < heap.length; i++)
{
this.heap[i] = heap[i];
idx = i;
}
}
}
참조 :
[자료구조] 힙(heap)이란 - Heee's Development Blog (gmlwjd9405.github.io)
'자료 구조' 카테고리의 다른 글
| 그래프와 트리의 정의와 차이점 (0) | 2023.01.31 |
|---|